Mit Hilfe der generativen Grafik können Bilder erzeugt werden. Die gewählten Algorithmen bestimmen die Bildklassen.
Selbst entwickelte Algorithmen können unterschiedlich parametrisiert werden, um unterschiedliche, künstlerisch ansprechende Bilder zuerstellen. Der optische Eindruck hängt von den Parameterngrenzen und dem Algorithmus ab. Können ni unterschiedliche Werte für den einen Parameter i gewählt werden, so schreiben wir ni ( i ). Es ergibt sich für mehrere Paramter die Bild-Anzahl = PRODUKT{ni(i)}, d.h. die Parameter-Variation liefert viele Bilder.
Wer kennt den Urgrund der Kunst?
Auch wenn viele Bilder automatisch erzeugt werden können, so ist die Bildauswahl nach künstlerischen, ästetischen Kriterien problematisch, schwierig und aufwendig. Die mit unterschiedlichen Parametereinstellungen erzeugten Bilder haben keine Gefühlszuordnung oder Bedeutung in der Kunst. Es gibt keine ästetischen Parameter und keine automatische Kunsthirachie.
Ein Mandala ist ein ästetisches Bild, das ein Zentrum hat, indem es eine individuelle, innere Weltsicht verkörpert.
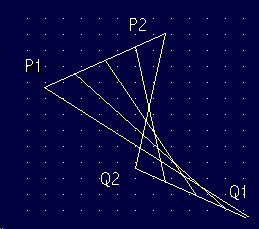
Die Punkte P(t) auf einer 1. Geraden durch 1, 2 können durch P(t) beschrieben werden. Der Parameter t läuft von 0 bis 1. Ebenso können die Punkte Q(t) auf einer 2. Geraden durch Q1, Q2 berechnet werden.

Die Punkte G(s) auf der Verbindungsgerade von P(t) nach Q(t) sind dann
Wird s = t und P(t) und Q(t) eingesetzt, so ist mit
Für 2:=1+(Q2-Q1), Q1:=Q2-(2-1) ergibt sich eine an 1, Q2 gespiegelte Kurve.
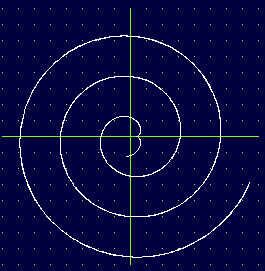
Spiralen werden in polaren Koordinaten ( r, t ) beschrieben durch
a ist eine Konstante und f(t) legt den Typ der Spirale fest. Durch
können polaren Koordinaten ( r, t ) in kartesische Koordinaten ( x, y ) umgerechnet werden.
Archimedische Spirale: f(t) = t
Ein Punkt P bewege sich mit konstanter Geschwindigkeit v
auf einem Halbstrahl von Anfangspunkt O weg nach außen.
Wenn der Halbstrahl mit konstanter Winkelgeschwindigkeit um O rotiert,
so beschreibt P eine Archimedische Spirale.
Hyperbolische Spirale: f(t) = 1/t
Die Hyperbolissche Spirale windet sich um O ( t -> 0 ), ohne diesen Punkt zu erreichen.
Eine Parallele im Abstand a zum Polstrah ist Asymptote.
logarithmische Spirale: f(t) = exp( m . t )
Ein Kreispunkt P hat von einem festen Kreispunkt ( r, 0 ) die Bogenlänge s. Wird s auf der Tangente in P abgetragen, so ergeben die Tangentenendpunkte die Kreisevolvente. Eine Evolvente schneidet diese Tangenten senkrecht.
Wenn ein geometrisches Objekt A auf der Oberfläche eines anderen Objektes A0 abrollt, so beschreibt ein fester Punkt von A eine Rollkurve. Das Abrollen soll ohne Gleiten und ohne Schlupf erfolgen. Oft wird ein Rad zum Abrollen verwendet ( Radkurven ).
Verlängerte und verkürzte Epi- und Hypo-Zykloide ( oder Epi- und Hypo-Trochoide ) sind Kurven, die von einem entweder außerhalb oder innerhalb eines Kreises befindlichen Punkt beschrieben werden, der sich auf einem vom Kreismittelpunkt ausgehenden und mit dem Kreis fest verbundenen Strahl befindet, während der Kreis an einem anderen Kreis entweder
abrollt, ohne dabei zu gleiten.
Wenn ein Kreis r auf einer waagerechten Geraden rollt, so beschreibt ein markierter Punkt k.r auf dem Radius des rollenden Kreises eine Zykloide.
x(t) = r . t - k . r . sin(t) y(t) = r - k . r . cos(t) |
Wenn ein Kreis r aussen auf einem Kreis R abrollt, so beschreibt ein markierter Punkt ( k.r ) auf dem Radius des rollenden Kreises eine Hypozykloide.
Epi-Trochoide ( r > 0 ), x(t) = ( R + r ) . cos( t ) - k . r . cos( (R+r).t/r ) y(t) = ( R + r ) . sin( t ) - k . r . sin( (R+r).t/r ) Speziell r = R ergibt sich eine Pascalsche Schnecke: x(t) = R . ( 2.cos(t) - k.cos(2.t) ) y(t) = R . ( 2.sin(t) - k.sin(2.t) ) |
| Epizykloiden | |
 gelb: R=1.5, r=1.0, k=1 |
 |
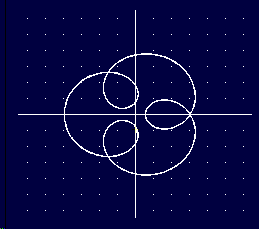 | weiss: R=1, r=R/k, k=4 |
Wenn ein Kreis r innen auf einem Kreis R abrollt, so beschreibt ein markierter Punkt ( k.r ) auf dem Radius des rollenden Kreises eine Hypozykloide.
Die Epi-Trochoide wird zur Trochoide, wenn "r" durch "-r" ersetzt wird.
x(t) = ( R - r ) . cos( t ) + k . r . cos(-(R-r).t/r ) y(t) = ( R - r ) . sin( t ) + k . r . sin(-(R-r).t/r )Speziell R = 2.r liefert eine Ellipse:
x(t) = r.(1+k).cos( t ) y(t) = r.(1-k).sin( t )
Ist t die Zeit, so kann die Bewegung eines Punktes auf dem Kreis r1 durch x(t) = r1 . cos(w1.t), y(t) = r1 . sin(w1.t) beschrieben werden. Wird der Kreis r1 selbst auf einem Kreis R0 bewegt, so ergeben sich die Kurven von Hipparchos (180-125 v.Chr.) und Ptolemäus ( ca. 150 n.Chr.).
x(t) = R0 . cos(w0 . t) + r1 . cos(w1 . t) y(t) = R0 . sin(w0 . t) + r1 . sin(w1 . t)
Ein zelluläre Automaten ist ein System von wechselwirkenden Zellen ( Komponenten ). Eine Zelle wird durch eine "Black Box" repräsentiert. Die Zellen haben innere Zustände C, die durch die Wechselwirkungen geändert werden.
Zelluläre Automaten können z.B quadratische Zellen von Satelliten-Bildern zugeordnet werden. Die Folge von Entwicklungen ( z.B. Ausbreitung von Feuer ) wird dann simuliert. Eine abgebrannte Zelle kann sich erholen. Es werden aufeinander folgende Zeitschritte t betrachtet. Einfache Regeln für die Wechselwirkungen der Zellen können z.B. wie folgt aussehen:
| Zustand der Zelle i | Bedeutung ( i, t ) |
| E | nackte Erde |
| G | Gras, Weideland |
| W | Wald |
| F | dichter Wald |
| Regeln | ( E, 0 ) ===> ( G, 1 ), ( G, 4 ) ===> ( W, 5 ), ( W, 39 ) ===> ( F, 40 ), ( i, t ) ===> ( E, 0 ) falls ein Feuer entzündet wird ( i, t ) ===> ( i, t+1 ) falls kein Feuer entzündet wird |
Ein linearer, zelluläre Automat besteht aus einer linearen Anordnung von Zellen. Der innere Zustand einer Zelle kann durch eine Variable ( Zahl, Matrix, Daten, Property ) beschrieben werden. Werden z.B. Weidegebiete betrachtet, so kann als Zustand einer Zelle durch die Anzahl von Schafen in der Zelle und das verfügbare, nachgewachsene Gras bestimmt sein.
Der Satz von Wechselwirkungen zwischen den Zellen werden als Regeln bezeichnet. Die Regeln bestimmen den aktuellen Zustand einer Zelle. Es ergeben sich zeitlich aufeinander folgende Zustände.
Die Zellen sind in einer Linie angeordnet ( lineare Anordnung, Kette, Array ). Meistens wird eine Zelle am stärksten durch die Nachbarzellen beeinflußt. Dadurch ergeben sich nachfolgende Arrays.
| C0 | C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | ... |
Für eine grafische Darstellung dieser aufeinander folgenden Arrays werden den aktuelle Zuständen eine Farbe zugeordnet.
Solche Zellen können in grober Näherung biologische Systeme beschreiben. Empirische Studien zeigen, dass unterschiedliche Fälle auftreten.
Die Zellen
Wenn nur wenige Regeln den Zustand einer Zelle ändern, so tendiert ein daraus folgendes Muster zu eingefrorenen, festen Endzuständen. Wenn viele Regeln den Zustand einer Zelle ändern, so tendiert ein daraus folgendes Muster zu einem gasähnlichem Verhalten.
| Zustände | Ci = 0 oder 1 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Nachbarn |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Regeln |
|
Wegen der besseren Übersicht wird "." anstelle von "0" geschrieben. Wird z.B. mit "..........1.........." begonnen, so ergeben sich die nachfolgenden Schritte:
| Step | Start mit ..........1.......... |
| 0 | ..........1.......... |
| 1 | .........111......... |
| 2 | ........1...1........ |
| 3 | .......111.111....... |
| 4 | ......1...1...1...... |
| 5 | .....111.111.111..... |
| 6 | ....1...1...1...1.... |
Anstelle von "..........1.........." kann auch mit einer Zufallsbesetzung begonnen werden.
import java.util.Random;
public class CellAut1D {
private int state_nr = 2;
private int radius_val = 1;
private long rule_nr = 2;
private int[] rule_tab = init_rule_tab( state_nr, radius_val, rule_nr );
public CellAut1D( int k, int r, long nr ) {
if ( state_nr != k || radius_val != r || rule_nr != nr ) {
if ( k > 1 ) state_nr = k;
if ( r >= 0 ) radius_val = r;
if ( nr >= 0 ) rule_nr = nr;
rule_tab = init_rule_tab( state_nr, radius_val, rule_nr );
}
}
public int[] ca_init( int n ) { // Generation of an initial configuration
Random random_number = new Random();
int[] array = new int[n];
for ( int i = 0; i < n; i++ ) {
array[i] = ( int ) ( state_nr * random_number.nextDouble() );
if ( array[i] > state_nr - 1 ) array[i] = state_nr - 1;
}
return array;
}
public int[] ca_next( int[] config ) {// Computing the next configuration
int len = config.length;
int[] res = new int[len];
for ( int i = 0; i < len; i++ ) { res[i] = 0;
for ( int j = -radius_val; j <= radius_val; j++ ) {
if ( i+j >= 0 && i+j < len ) res[i] += config[i+j];
else
if (i+j < 0) res[i] += config[len-i+j];
else res[i] += config[i+j-len];
}
res[i] = rule_tab[res[i]];
}
return res;
}
private int[] init_rule_tab( int k, int r, long nr ) {// Construction of the rule table
int n = ( k - 1 ) * ( 2 * r + 1 ) + 1;
int[] table = new int[n];
for ( int i = 1; i <= n; i++ )
table[i-1] = rule_value( i, nr, k );
return table;
}
private int rule_value( int b, long n, int k ) {// Help routine for making rule tables
if ( b == 1 ) return (int)( n % k );
else return rule_value( b-1, n/k, k );
}
}
Die Zellen sind in einer ebenen Fläche angeordnet ( 2D-Gitter, 2D-Array ). Meistens wird eine Zelle am stärksten durch die Nachbarzellen beeinflußt. Dadurch ergeben sich nachfolgende 2D-Arrays. Der innere Zustand einer Zelle Ci kann durch eine Variable ( Variable, Zahl-Representation, Matrix-Representation, Daten-Representation, Property ) beschrieben werden.
Werden z.B. Weidegebiete Ci betrachtet, so kann als Zustand einer Zelle durch die Anzahl von Schafen im Weidegebiet und das verfügbare, nachgewachsene Gras bestimmt sein.
Bei einem 2D - Gitter werden Zellen in einer Ebene betrachtet. Es gibt unterschiedliche 2D - Nachbarschaften. Ist Cj die betrachtete Zelle, so können Nachbarzellen Ci auf die Zelle Cj einwirken. Der Zustand von Cj wird dadurch geändert.
| Vierer- Umgebung ( U4 ) | Achter- Umgebung ( U8 ) | unsymetrische- Umgebung | |||||||||||||||||||||||||||||||||
|
|
|
Die folgenden Regeln wurden von Wolfram u.a. empirisch untersucht. Das Game of LIFE kann eine von Neumann - Automaten ( digitalen Computer ) abbilden.
| Anzahl der Nachbarn | 1=lebende 0=tote Zelle | 1=lebende 0=tote Zelle | ||
| 0 | 1 | ===> | 0 | lebende Zelle stirbt |
| 1 | 1 | ===> | 0 | lebende Zelle stirbt |
| 2 | keine Änderung | |||
| 3 | 0 | ===> | 1 | tote Zelle lebt wieder |
| 4 | keine Änderung | |||
| 5 | 1 | ===> | 0 | lebende Zelle stirbt |
| 6 | 1 | ===> | 0 | lebende Zelle stirbt |
| 7 | 1 | ===> | 0 | lebende Zelle stirbt |
| 8 | 1 | ===> | 0 | lebende Zelle stirbt |
Es wird mit einer initialisierten Startkonfiguration ( Muster ) gestartet. Es entstehen
| => |
| => |
|
Viele natürliche Objekte wie z.B. Berge, Bäume, Küstenlinien weisen eine rauhen, zackigen Rand auf. Ein "glatter" Rand kann durch differenziebare Funktionen angenähert werden. Dagegen führen bei natürlichen Objekten Verfeinerungen ( magroskopisch, molekular, atomar, Elementarteilchen, usw. ) zu immer neuen Rändern.
Vielfach ist die Natur selbstähnlich. Z.B. ist der Ast eines Baumes wieder so aufgebaut wie der Baum. Das Leben reproduziert sich selbst.
Mandelbrot, Hausdorff, Julia prägten ( etwa 1977 ) den Begriff "Fraktal". Fraktal ist eine Abkürzung für "fractional dimension".
Im Gegensatz zu glatten mathematischen Kurven besitzen fraktale Kurven keine Steigung und überall Knicke. Fraktale Kurven sind stetig aber nicht differenzierbar. Die Struktur eines Fraktals ändern sich, sobald der Maßstab geändert wird. Definition:
| D = Fraktale Dimension, Li=Masszahl mit Skalenlänge Si |
ln ( L2 / L1 )
D = ---------------
ln ( S1 / S2 )
|
Mit einer Messlatte kann die Länge der Küste von England gemessen werden. Je kürzer die Messlatte, umso größer wird die Länge.
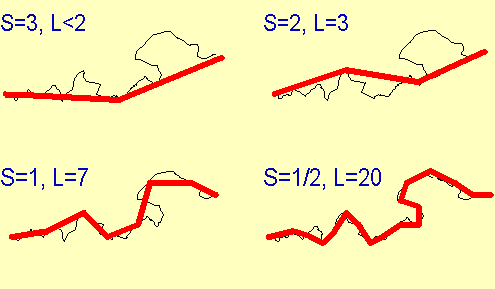
Für S1=0.5 bzw. S2=1.0 ergebe sich L1=20 bzw. L2=7. Dann wird D=ln(20/7)/ln(2) = 1.51 Für S1=1.0 bzw. S2=2.0 ergebe sich L1=7 bzw. L2=3. Dann wird D = 1.22 Für S1=2.0 bzw. S2=3.0 ergebe sich L1=3 bzw. L2=2. Dann wird D = 1.13 Küsten haben etwa die empirische Dimension D = 1.15 .. 1.25 Arterien haben etwa die empirische Dimension D = 2.7
Wird ein Rechteck ( L1=1, S1=1.0 ) in 4 gleiche Teilrechtecke ( L2=4, S2=0.5 ) und dann jedes Teilrechteck in 4 noch kleinere Sub-Teilrechtecke ( L3=16, S3=0.25 ) unterteilt, so ergibt sich als Dimension des Rechtecks 2:
ln( 4 / 1 ) ln( 16 / 4 )
D = --------------- = ---------------- = 2
ln( 1.0/0.5 ) ln( 0.5/0.25 )
|
| Rechteck L1=1 in 4 gleiche Teilrechtecke L2=4 unterteilt |
Jedes Teilrechteck L2 in 4 gleiche Sub-Teilrechtecke L3=16 unterteilt |
Die Dimension der folgenden Endfigur ist 1.46497:
ln ( L2 / L1 ) ln( 5 / 1 ) ln( 25 / 5 )
D = --------------- = --------------- = ---------------- = 1.46497
ln ( S1 / S2 ) ln( 1.0/.333) ln( .333/.111 )
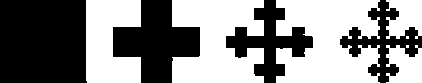
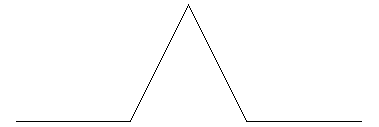
Bei der Koch - Kurve ( Schneeflocke ) wird eine Strecke in 3 gleiche Teile geteilt. Das mittlere Stück herausgenommen und gknickt, verdoppelt wieder eingefügt. Es ist D = ln(4)/ln(3) = 1.2619
M3
/\
_______ wird ersetzt durch ___ / \___
P1 P2 M1 M2
| |
| Stufe 0 | Stufe 1 |
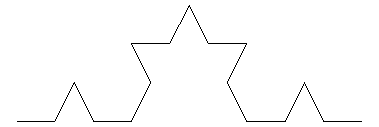
| |
| Stufe 2 | Stufe 3 |
| Stufe 4 | Stufe 5 |
Der folgende Pseudocode zeichnet eine Koch-Kurve. D1, D2 sind kleine Auslenkungen von M1, M2.
Koch( P1, P2 ) {
falls | P2 - P1 | > Epsilon {
M1 = ( 2.P1 + P2 )/3 + D1;
M2 = ( P1 + 2.P2 )/3 + D2;
M3 = Konstrukt( M1, M2);
Koch( P1, M1 );
Koch( M1, M3 );
Koch( M3, M2 );
Koch( M2, P2 );
} else {
draw( P1, P2 );
}
}
Zu dem Sierpinski-Dreieck ( Pole, Waclaw Sierpinski 1892-1969 ) gehört eine kontrahierende Ähnlichkeitsabbildung.
| Aus dem einen Dreieck
( a b c ) werden die folgenden 3 Dreiecke | ||
| ( a ab/2 ac/2 ) | ( 1.0 .0 .0 ) ( .0 0.5 .0 ) ( .0 .0 0.5 ) | |
| ( ba/2 b bc/2 ) | ( 1.0 .0 .0 ) ( 0.5 0.5 .0 ) ( .0 .0 .5 ) | |
| ( ca/2 cb/2 c ) |
( 1.0 .0 .0 ) ( 0.25 0.5 .0 ) ( 0.25/sqrt(3) .0 0.5 ) | |
Durch diese Abbildungen entstehen aus einem Dreieck jeweils 3 neue Dreiecke. Das alte Dreieck wird dann nicht mehr benötigt.
| Konstruktionsprinzip | Sierpinski-Dreieck |
Das Dreieck A ( rot ) , B ( blau ) , C ( gelb ) ist gegeben. Wie entsteht das Dreieck?
Affine 2D - Abbildungen können durch
x' = a . x + b . y + e ( 1 ) ( 1 0 0 ) ( 1 )
oder ( x') = ( e a b ) . ( x )
y' = c . x + d . y + f ( x') ( f c d ) ( y )
MatrizenSchreibweise
X' = A . X
|
beschrieben werden. Durch A wird ein Punkt ( x, y ) in den Für diese Affine 2D - Abbildungen gilt
Eine selbstähnliche Figur wird aus
Das Aussehen einer selbstähnlichen Figur bleibt bei einer Änderung des Maßstabes ungeändert. Mit Zufallsiterationen ( random iteration algorithms ) können fraktale Bilder erzeugt werden. Das iterierte Funktionensysteme X' = A . X ( abgekürzt IFS )
x' = a . x + b . y + e ( 1 ) ( 1 0 0 ) ( 1 )
oder ( x') = ( e a b ) . ( x )
y' = c . x + d . y + f ( x') ( f c d ) ( y )
MatrizenSchreibweise
X' = A . X
|
kann wiederholt angewendet werden X' = ... A3.A2.A1.A0 . X Dabei kann jede Matrix Ak unterschiedliche Koeffizienten haben.
Wird nach jeder Anwendung von unterschiedlichen Ak der neue Punkt X' grafisch dargestellt, so ergibt sich die Punktmenge ein Bild, das gegen den Attraktor des IFS konvergiert. Die Häufigkeit der Abbildung Ak ist durch die Wahrscheinlichkeit k festgelegt. Die Summe aller Wahrscheinlichkeiten ist 1.
------------------------------------------------------------
Parameter
k ak bk ck dk ek fk k
--------------------------------------------------------------------------------
Koch 1 0.3333 0 0 0.3333 0 0 0.25
1 0.3333 0 0 0.3333 0.6667 0 0.25
2 0.1667 -0.28867 0.28867 0.1667 0.3333 0 0.25
3 -0.1667 0.28867 0.28867 0.1667 0.6667 0 0.25
--------------------------------------------------------------------------------
|
Pseudocode: Koch-Kurve
//k = 0 1 2 3
a[] = { 0.3333,0.3333,0.1667,-0.1667 };
b[] = { 0, 0, -0.28867,0.28867};
c[] = { 0, 0, 0.28867,0.28867};
d[] = { 0.3333,0.3333,0.1667, 0.1667 };
e[] = { 0, 0.6667,0.3333, 0.6667 };
f[] = { 0, 0, 0, 0 };
x = y = 0;
for ( i=0; i < 80000; i++ ) {
k = i % 4; /* alle Abb. gleichwahrscheinlich */
h = a[k] * x + b[k] * y + e[k];
y = c[k] * x + d[k] * y + f[k];
x = h;
setPixel( 20+(int)(600*x), 300-(int)(600*y) );
}
Pseudocode: Sierpinski-IFS
a[] = { 0.5 ,0.5, 0.5, 0 };
b[] = { 0, 0, 0, 0 };
c[] = { 0, 0, 0, 0 };
d[] = { 0.5, 0.5, 0.5, 0 };
e[] = { 75, 0, 150, 0 };
f[] = { 0, 150, 150, 0 };
for i=0 to 299 {
setPixel(i+150, 0); setPixel(i+150, 299);
setPixel( 449, i); setPixel( 150, i);
for iter :=0 to 8 {
for i:=0 to 300 {
for j:=0 to 300 {
color := getPixel( i+150, j );
if color == 0 continue;
for k:=0 to 2 do
n := Round( a[k]*i + b[k]*j + e[k] );
m := Round( c[k]*i + d[k]*j + f[k] );
setPixel( n+150, m );
}
}
}
}
}
Ein Farn kann z.B. mit 4 Abbildungen erzeugt werden. Jede Abbildung sollte mit ihrer Wahrscheinlichkeit p aufgerufen werden. Die Wahrscheinlichkeit p gibt an, wie häufig eine Abbildung Ak ( X' = ... A3.A2.A1.A0 . X ) aufgerufen wird. Das erzeugte Bild entspricht einem gewichteten Zufallsweg.
------------------------------------------------------------
Parameter
k ak bk ck dk ek fk k
--------------------------------------------------------------------------------
Farn1 0 0.0 0.0 0.0 0.16 0.0 0.0 0.10
1 0.2 -0.26 0.23 0.22 0.0 1.6 0.08
2 -0.15 0.28 0.26 0.24 0.0 0.44 0.08
3 0.75 0.04 -0.04 0.85 0.0 1.6 0.74
--------------------------------------------------------------------------------
Farn2 0 0.0 0.0 0.0 0.16 0.0 0.0 0.03
1 0.197 -0.026 0.226 0.197 0.0 1.6 0.08
2 -0.155 0.283 0.26 0.237 0.0 0.44 0.11
3 0.849 0.037 -0.037 0.849 0.0 1.6 0.73
--------------------------------------------------------------------------------
Gras 0 0.0 0.0 0.0 0.5 0.0 0.0 0.15
1 0.02 -0.28 0.15 0.2 0.0 1.5 0.10
2 0.02 0.28 0.15 0.2 0.0 1.5 0.10
3 0.75 0.0 0.0 0.5 0.0 4.6 0.65
-------------------------------------------------------------------------------------------------
Baum k ak bk ck dk ek fk k
0 0.008574875 -0.12698 0.005351281 0.2034723 0.5239437 0.1684814 0.07257033
1 0.4481037 0.5286823 -0.2171193 0.5338841 0.2934272 0.4904489 0.19262947
2 0.01180531 -0.002232286 7.066541e-5 0.3729313 0.5114241 0.01948435 0.0964392
3 -0.04473789 -0.4193087 0.4365308 -0.04297287 0.4808853 0.09414654 0.1542334
4 0.6313646 -0.1370768 0.1302645 0.6643821 0.1062206 0.2367478 0.2404008
5 0.2710752 0.345816 -0.2492639 0.3760758 0.3630673 0.3575294 0.1263472
6 -0.1150927 0.2965249 -0.2193086 -0.1556157 0.6242567 0.4381089 0.0916967
7 0.01648819 0 0 0.06127364 0.5087495 0.02214118 0.0256829
-------------------------------------------------------------------------------------------------
Ist detak = ak . dk - bk . ck die Determinante der Abbildung, so können die Wahrscheinlichkeiten empirisch durch k = detk / Summe_aller( detk ) berechnet werden.
Der folgende Pseudocode zeigt die Verwendung der Koeffizienten a[k], b[k], c[k], d[k], e[k], f[k] als stochastischer IFS-Algorithmus nach Michael Barnsley: Fractals Everywhere Academic Press, San Diego 1988, p.91
Pseudocode:
//k = 0 1 2 3
a[] = ( 0, 0.197,-0.15, 0.849 );
b[] = ( 0, -0.226, 0.283, 0.037 );
c[] = ( 0, 0.226, 0.26, -0.037 );
d[] = ( 0.16, 0.197, 0.237, 0.849 );
e[] = ( 0, 0, 0, 0 );
f[] = ( 0, 1.6, 0.44, 1.6 );
p[] = ( 0.03, 0.13, 0.11, 0.73 );
x = y = 0;
for i= 1 to 75000 {
pk = random; k = 0; s = p[0];
while ( s /lt; pk ) { k ++; s += p[k]; }
h := a[k] * x + b[k] * y + e[k];
y := c[k] * x + d[k] * y + f[k];
x := h;
setPixel( round(x*50) + 300, 430 - round(y*40) );
}
Wird jede affine Abbildung Ak mit einer bestimmten Farbe gezeichnet, so zerfällt das gesamte Bild in die Teilstrukturen ( Collage-Theorem ). Das Zusammensetzen erfolgt lückenlos.
Die Funktion countMandel() ermittelt zu dem vorgegebenen Start-Punkt Z0 = x0 + i.y0 die Anzahl von Iterations- Schritten, bis Divergenz festgestellt wird. Ist der Rueckgabe-Wert gleich MaxCount, so soll Konvergenz angenommen werden.
static public int countMandel( int MaxCount, double x0, double y0 ) {
int anz = 0 ; double h ; double r2 = 0.0 ;
double x = x0 ;
double y = y0 ;
while ( ( anz < MaxCount ) && ( r2 < 4.0 ) ) { h = x ;
x = x * x - y * y ; x += x0 ;
y = h * y ; y += y ; y += y0 ;
r2 = x * x + y * y ;
anz ++ ;
}
return anz ;
}
Die Funktion countMandel() wird oft aufgerufen. Deshalb ergibt jede Einsparung an Multiplikationen einen zeitlichen Gewinn. Z.B. kann anstelle von r2 = x * x + y * y; ( r2 - Schranke 4.0 ) auch
xx = fabs( x ) ; yy = fabs( y ) ; if ( xx < yy ) r2 = xx + yy + yy + yy ; else r2 = yy + xx + xx + xx ;
mit der r2 - Schranke 12.0 verwendet werden. Zum Zeichnen der Z=Z^2+C - Fraktale ( Mandelbrod-Menge ) dient drawMandel():
static public void drawMandel( int MaxCount, double xMin, double yMin, double xMax, double yMax )
{ int i, j, di, dj ; double x0,y0 ; int anz ; Color col ;
bG.setSpaceRxy( xMin,yMin, xMax,yMax );
di = dj = 1 + 20 / MaxCount ;
for ( j = bG.jMin ; j <= bG.jMax ; j += dj ) { y0 = y_from_j( j ) ;
for ( i = bG.iMin ; i <= bG.iMax ; i += di ) { x0 = x_from_i( i ) ;
anz = countMandel( MaxCount, x0, y0 ) ;
if ( anz >= MaxCount ) drawLine( i, j, i+di, j ) ;
}
}
}
Den Funktionen x_from_i( i ), y_from_j( j ) entspricht die Umrechnung:
x0 = xMin + ( xMax - xMin ) * i / iMax y0 = yMax + ( yMin - yMax ) * j / jMax
wobei iMin = jMin = 0 ist.
Zum Zeichnen der Mandelbrod-Menge kann z.B. drawMandel( 20, -1.8, -1.5, 1.2, 1.5 ) aufgerufen werden.
Die berechneten Schritt-Anzahlen anz = countMandel() soll als Farbe benutzt werden.
Die Julia-Mengen ist die Mengen aller Punkte P(z) = z2 + c für die der Grenzwert der iterierten Abbildung beschränkt bleibt ( z = x + i y, c = a + i . b ) .
Startwert für z: a b
--------------------------------------
Fatou Staub 0.11031 0.67037
San Marco -1.0 0
Julia Drache 0.360284 0
Douadys Kaninchen -0.122 0.745
Dentrit 0 1
Misiurewicz-Punkt -0.101 0.9563
--------------------------------------
xmax=1.4; ymax= 1.4;
a=-0.11031; b= 0.67037; //Fatou Staub
n1 = 250;
n2 = (int) (n1 * ymax / xmax);
eps = xmax/n1;
for ( i=0; i <= n1; i++ )
for ( j=-n2; j <= n2; j++ ) {
if ( i == 0 && j == 0 ) break;
x = i * eps; y = j * ymax/n2;
u = 1; v = 0;
for ( k = 0; k <= 200; k++ ) {
x1 = x * x - y * y + a;
y1 = 2 * x * y + b;
u1 = 2 * ( u * x - v * y);
v1 = 2 * ( u * y + v * x);
s1 = x1 * x1 + y1 * y1 + 1.e-10;
s2 = log(s1);
s3 = sqrt( u1 * u1 + v1 * v1 + 1.e-10 );
if (( s1 > 50.) || ( s3 > 50. )) {
dist = sqrt(s1) * s2 / s3;
if ( dist < eps ) { //Color 1+k/20
setPixel( 320+i, 240-j );
setPixel( 320-i, 240+j );
}
break;
}
x = x1; y = y1; u = u1; v = v1;
}
}
Bäume sind oft selbstähnlich. Ein Ast ist wie der Baum aufgebaut. Die Selbstähnlichkeit wird oft in der Natur angetroffen. Leben ( Menschen, Tiere, Pflanzen ) versuchen sich selbst zu reproduzieren.
Der Biologe Aristid Lindenmayer ( L-System ) hat etwa 1930 ein Modell ( formale Grammatik ) für das Pflanzenwachstum entwickelt. In dem Grammatik-Modell werden alle Produktionen gleichzeitig angewendet. Die erzeugten Worte werden z.B. als topologische Struktur einer Planze interpretiert.
| benutzte Symbole | Erklärung | Beispiel |
| Variablen | können ersetzt werden | |
| Konstanten | Symbole, die nicht geändert werden | Jede gramatikalische Variable <subject> <verb> <predicate> kann durch Worte ersetzt werden. Es ergeben sich Sätze, wie z.B. "Die Katze ist grau" |
| Start- Regeln | <Satz> | |
| Syntax- Regeln | Ersetzungen | <subject> ===> "Die Katze" |
| Variablen | A B |
| Konstanten | keine |
| Start | A |
| Regeln |
B ===> AB A ===> B |
| Beispiel | Step 0 : A Length = 1 Step 1 : B Length = 1 Step 2 : AB Length = 2 Step 3 : BAB Length = 3 Step 4 : ABBAB Length = 5 Step 5 : BABABBAB Length = 8 Step 6 : ABBABBABABBAB Length = 13 Step 7 : BABABBABABBABBABABBAB Length = 21 |
| Variablen | A B B D |
| Konstanten | keine |
| Start | A |
| Regeln |
A ===> DB B ===> C C ===> D D ===> E E ===> A |
| Beispiel | Step 0 : A
Step 1 : D B
Step 2 : E C
Step 3 : A D
Step 4 : D B E
Step 5 : E C A
Step 6 : A D D B
Step 7 : D B E E C
Step 8 : E C A A D
Step 9 : A D D B D B E
Step10 : D B E E C E C A
Step11 : E C A A D A D D B
|
Ein Laubbaum besteht aus Ästen und Blättern. A sei ein Aststück und B ein Blatt. Ein mit 45o abstehender Ast wird durch die Klammerung ( ) gekennzeichnet.
| Variablen: | A = Aststück, B = Blatt |
| Konstanten: | ( ) für 45o Abzweigung |
| Start: | B |
| Regeln: | A ===> AA B ===> AA(B)A(B) |
| Beispiel: |
Step 0 : B
Step 1 : AA(B)A(B)
Step 2 : AAAA(AA(B)A(B))AA(AA(B)A(B))
|
|
|
|
Es wird der Weg einer Schildkröte in der x,y-Ebene beschrieben. Die Schildkröte kann in der aktuellen Situation n Schritte gehen.
Die Konstanten dienen zum Zeichnen der Figur.
| Variablen | {, , , ...} |
| Konstanten | { nF, nB, aR, aL, stop } |
| Start | Punkt in der Ebene |
| Regeln | <Path> ===> nF <Path> <Path> ===> nF aR <Path> <Path> ===> nF nB <Path> <Path> ===> nF aL <Path> <Path> ===> nF stop |
| Beispiel | "4F 90R F 90R F 90R "
|
| Beispiel Farn | <Path> ===> <Design> stop <Design> ===> 4 <Arm> <Arm> ===> 4F 3<Corner> 1F <Corner> ===> 2F 3<Turn> <Turn> ===> 90R F |
Das Programm FRACTINT benutzt die folgende Syntax:
Leaf1 { ; Name of the l-system, "{" indicates start
; Compound leaf with alternating branches,
angle 8 ; Set angle increment to (360/8)=45 degrees
axiom x ; Starting character string
a=n ; Change every "a" into an "n"
n=o ; Likewise change "n" to "o" etc ...
o=p
p=x
b=e
e=h
h=j
j=y
x=F[+A(4)]Fy ; Change every "x" into "F[+A(4)]Fy"
y=F[-B(4)]Fx ; Change every "y" into "F[-B(4)]Fx"
F=@1.18F@i1.18
} ; final } indicates end