Malerei, bildende Kunst in Antike ( Theater- und Wandmalerei, Raumtiefe und Verkürzungen nach 'Gefühl" );
Masaccio ( 1425, konstruiertes Fresko in Santa Maria Novella in Florenz, Figuren und Raum sind erstmals auf den Ort des Betrachterortes bezogen );
Masaccio: Freskenzyklus der Brancacci-Kapelle in Santa Maria del Carmine in Florenz,
Szenen aus dem Leben Petri, Szene: Erweckung des Sohnes des Theophilus,
Fürst von Antiochien und Petrus in Kathedra.
1425-1428, Fresko. Florenz, Santa Maria del Carmine, Cappella Brancacci.
Kommentar: Fresken unter Mitarbeit von Masolino entstanden, fertiggestellt durch Filippino Lippi.
Land: Italien. Stil: Renaissance.
Filippo Brunelleschi ( um 1420, Florenz ) hat die Linearperspektive neu 'erfunden';
Leon Battista Alberti ( um 1435 ) erschafft ein Theorie der Pektive; Perspektive wurde wissenschaftliche Disziplin; Lehrstühle für 'Glastafelverfahren': Frontparallele Glasplatte zwischen Betrachter und Gegenstand;
Intarsien-Kunst [italienisch] ( in Holz eingelegte Verzierungen aus Holz, Bein, Schildpatt, Perlmutter, Metall, Stein );
Veduten-Malerei [italienisch] ( topograph. getreue Wiedergabe, Stadt, Landschaft );
Paolo Uccello ( Florenz ), Piero della Francesca ( San Sepolcro ); Ambrogio Lorenzetti in Siena, erschaffte erstmals ( 1.Hälfte 14.Jh. ) einen 'modernen' Systemraum mit Raumtiefe genäss den Sehgewohnheiten );
Im Norden Europas: Michael Pacher, Albrecht Dürer ( konstruierte eine Lichtstahl-Apparat ) Jan van Eyck ( Dartsellung von Innenräumen, Anamorphosen [ Abweichungen ] verstärken das subjektives Raum- und Realitätsempfinden;
Leonardo da Vinci ( verschiedene Fluchtpunkte ) Nah- und Fernwirkung der Farbwerte. Verblauen und Verblassen der Farben in der Bildtiefe;
Venezianische Malerei ( 16.-18.Jh., z.B. Tintoretto in Venedig schafft vielschichtige Raummodellen mit ungewohnt moderner Sturzperspektiven;
Niederländische Landschaftsmalerei ( 17.Jh. );
Im 19.Jh zunehmend illusionistische Bilder. ( Kamera machte Fotografische Abbildung );
Paul Cézanne ( Beweglichkeit des Auges, verschiedener Blickpunkte );
Moderne Malerei ersetzte die perspektivische Konstruktionen durch a-perspektivische Methoden mit Flächenkomposition und Farbraum ( Expressionismus, Fauvismus, Kubismus ). Die Surrealisten stellen surreale oder Traumräume dar.
Die Projektionen können eingeteilt werden in Projektionen mit konvergierenden bzw. parallele Projektionsstrahlen.
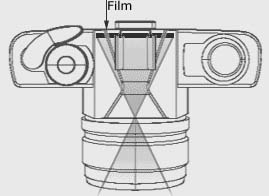
| Kamera ( lat. Camera obscura), Gerät zur photographischen Abbildung der sichtbaren Wirklichkeit mit Licht | |
|
|
Unterschiedliche Standorte des Betrachters ergeben die Vorder - Ansicht, die Seiten - Ansicht, die Drauf - Sicht eines Körpers. Wie können die Punkte P( u, v ) in der Zeichen - Ebene berechnet werden, wenn alle Raum - Punkte P( x, y, z ) eines Körpers bekannt sind?
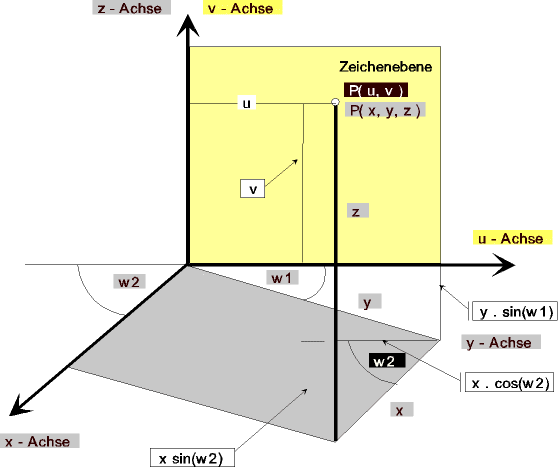
Ein Raumpunkt P ( x, y, z ) wird auf die Zeichen - Ebene abgebildet. In der Zeichenebene hat der Punkt die Koordinaten ( u, v ). Mit den Winkel w1, w2 setzt sich die horizontale Strecke u zusammen aus y . cos(w1) - x . cos(w2). Die vertikale Strecke v ergibt sich durch z - y . sin(w1) - x . sin(w2).
u = - x . cos(w2) + y . cos(w1), v = - x . sin(w2) - y . sin(w1) + zSollen die x, y - Werte gestaucht werden, so werden Faktoren ux, uy,vx, vy eingeführt.
u = - x . ux . cos(w2) + y . uy . cos(w1) , v = - x . vx . sin(w2) - y . vy . sin(w1) + z
| Dimetrie ( Höhen erscheinen in wahrer Größe ) | w1 = 7.18° | w2 = 41.43° | ux = 0.5, uy = 1.0, vx = 0.5, vy = 1.0 |
| Isometrie ( Höhen erscheinen in wahrer Größe ) | w1 = 30.0° | w2 = 30.0° | ux = 1.0, uy = 1.0, vx = 1.0, vy = 1.0 |
| Kavalierperspektive ( Vorderansichten erscheinen in wahrer Größe ) | w1 = 0.0° | w2 = 45.0° | ux = 0.5, uy = 1.0, vx = 0.5, vy = 1.0 |
| Militärperspektive ( Grundflächen erscheinen in wahrer Größe ) | w1 = 45.0° | w2 = 45.0° | ux = 1.0, uy = 1.0, vx = 1.0, vy = 1.0 |
Besonders einfache Isometrie - Formeln ergeben sich für w1 = 30.0°, w2 = 30.0° ux = uy = 2/sqrt(3), vx = vy = 1.0
3D - SPIELE u = y - x , v = z - ( x + y ) / 2
Dies entspricht einer 4x4 - Matrizen - Multiplikation:
( u ) ( -1 1 0 0 ) ( x ) ( v ) = (-1/2 -1/2 1 0 ) . ( y ) ( w ) ( 0 0 1 0 ) ( z ) ( 1 ) ( 0 0 0 0 ) ( 1 )
Die Determinante dieser 4x4 - Matrix ist 1. Diese Projektion hat dann besondere Vorteile, wenn gerätespezifisch ( Pixel ) auf ganzen Zahlen operiert wird ( 3D - Spiele ). Die Division wird durch eine schnelle Shift - Operation ersetzt. Dadurch ergeben sich kurze Ausführungszeiten.
Eine speziell orthogonale Projektion liegt vor, wenn anstelle von u = y - x, v = z - ( x + y ) / 2 die etwas geänderte Projektion
u = y - x , v = z - ( x + y ) / sqrt(2)
benutzt wird. Die ( nicht normierten ) Richtungs - Vektoren der Zeichenebene sind dann
U = ( -1, 1, 0 )´ V = ( -sqrt(1/2), sqrt(1/2), 1 )´ W = ( 1, 1, sqrt(2) )´
Der Vektor W entspricht dem Normalen - Vektor der Zeichen - Ebene. Zur Berechnung der Sichtbarkeit wird W benötigt.
Achtung! Die Winkelbezeichnung w1, w2 bedeutet hier Winkel für die Kugelkoordinaten. Die Winkel w1, w2 sind verschieden von den obigen 2D - w1, w2 - Winkeln von Isometrie, Dimetrie, Kavalierperspektive, Militärperspektive.
Die Lage eines Punktes P(x, y, z) auf einer Kugel kann durch die Angabe von r, w1, w2 erfolgen. Die r -, w1 -, w2 - Bereiche sind: 0 <= r, 0 <= w1 < 2 pi, 0 <= w2 <= pi
x = r . sin(w2) . cos(w1) , 0 <= r, y = r . sin(w2) . sin(w1) , mit 0 <= w1 < 2 pi, z = r . cos(w2) 0 <= w2 <= pi
Hierbei ist der Kugel - Mittelpunkt P0( 0, 0, 0). Der Kugelradius ist r. Bei der "Erdkugel" entspricht die geographischen Länge dem Winkel w1 und die geographische Breite dem Winkel ( w2 - pi/2 ). Durch einen Punkt P(x, y, z) auf der Einheitskugel ( r = 1 )
x = sin(w2) . cos(w1) , 0 <= u, y = sin(w2) . sin(w1) , mit 0 <= w1 < 2 pi, z = cos(w2) 0 <= w2 <= pi
gehen Längen - und Breiten - Kreise. Zusammen mit der Radius - Verlängerung ergibt sich daraus ein lokales Koordinaten - System im Punkt P(x,y,z). Die partiellen Ableitungen ( von P nach w2 ), ( von P nach w1 ) / sin(w2), und P selbst ergeben die Matrix
( c2.c1 -s1 s2.c1 ) ( c2.s1 c1 s2.s1 ) ( -s2 0 c2 )
wobei c1 = cos(w1), c2 = cos(w2), s1 = sin(w1), s2 = sin(w2) ist. Die Matrix ist durch die beiden Winkel w1, w2 festgelegt.
( c2.c1 c2.s1 -s2 ) ( -s1 c1 0 ) ( s2.c1 s2.s1 c2 )
Die Determinante ist (c12 + s12 ) .(c22 + s22 ) = 1. Die Beträge jeder Spalte und Zeile sind 1. Die inverse Matrix ergibt sich durch die Spiegelung der Matrix - Elemente an der Hauptdiagonalen. Mit den Faktoren
ux = -sin(w1), uy = cos(w1) , vx = cos(w1).sin(w2), vy = sin(w1).sin(w2), vz = cos(w2)ergeben sich die Formeln für die orthogonale Projektion
u = ux . x + uy . y , v = vx . x + vy . y + vz . z
Die ux, uy, vx, vy, vz - Zahlen werden einmal berechnet. Dann werden i.a. viele 3D - Punkte P( x, y, z )
in die 2D - Punkte ( u, v ) der Zeichen - Ebene umgerechnet.
Der Vektor W = ( c2.c1, c2.s1, -s2 )´ entspricht dem Normalen - Vektor der Zeichen - Ebene.
W wird zur Sichtbarkeit - Berechnung von P benötigt.
Speziell für die Winkel w1 = 45°, w2 = - 45° ergibt sich
u = ( y - x )/sqrt(2) , v = -( x + y )/2 + z/sqrt(2)oder anders skaliert
u = y - x , v = z - ( x + y ) / sqrt(2)
Die ( u, v ) - Werte entsprechen den 2D - Bild - Koordinaten des 3D - Punktes P(x, y, z). Der Vektor W = ( 1, 1, sqrt(2) )´ entspricht dem Normalen - Vektor der Zeichen - Ebene. W wird zur Berechnung der Sichtbarkeit von P benötigt.
Die orthogonale Projektion soll den 3D - Punkt bRxyz P in den Bildpunkt B um rechnen. Hierzu soll bRxyz B = P.Projektion() verwendet werden. Von B werden lediglich die Komponenten B.x, B.y verwendet.
Die überladene Funktion Projektion( w1, w2 ) hat keinen Rückgabewert. Es werden lediglich die static Variablen U, V, W der Zeichenebene berechnet und gespeichert. W entspricht der Haupt - Blickrichtung.
public class bRxyz extends Object { //bRxyz - Klasse
public double x, y, z; //aktueller Punkt
static public bRxyz U, V, W; //Zeichenebene
static private boolean isNotInit = true; //
public bRxyz( double x, double y, double z ){//Konstruktor
if ( isNotInit ) Projektion( 45.0, -45.0 );
this.x = x; this.y = y; this.z = z;
}
static public void Projektion( double w1, double w2 ) {
double x, y, z; U = V = W = null; isNotInit = false;
w1 = w1/180*Math.PI; w2 = w2/180*Math.PI; //in Bogenmass
x =-Math.sin(w1);
y = Math.cos(w1); //Zeichenebene U, V, W
z = 0.0; U = new bRxyz(x, y, z);
x = Math.cos(w1)*Math.sin(w2);
y = Math.sin(w1)*Math.sin(w2); //Zeichenebene U, V, W
z = Math.cos(w2); V = new bRxyz(x, y, z);
x = Math.cos(w1)*Math.cos(w2); //Zeichenebene U, V, W
y = Math.sin(w1)*Math.cos(w2); //W ist die Normale
z = -Math.sin(w2); W = new bRxyz(x, y, z);
}
public bRxyz Projektion( ) {
if ( isNotInit ) Projektion( 45.0, -45.0 );
double u = U.x * this.x + U.y * this.y ;
double v = V.x * this.x + V.y * this.y + V.z * this.z ;
return ( new bRxyz(u,v,0) );
}
};
Eine perspektivische Projektion bildet mit Hilfe von Matrizen-Multiplikationen die Geometrie eines 3D - Objektes ( Model - Space ) auf ein "Einheitsvolumen" ab, das dann die reelle 2D - Ebene ( Projection Plane, Zeichenfläche ) ergibt. Speziell bei der orthogonalen Projektion wird ein (x2,y2,z2)-(x1,y1,z1)-Quader auf das (1,1,1)-(-1,-1,-1)-Volumen abgebildet. Z.B. kann für den (x2,y2,z2)-(x1,y1,z1)-Quader der alle Objekte umfassende Quader gewählt werden.
Die beiden folgenden Matrizen sind invers zueinander, d.h. es ist die 4x4 Einheitsmatrix = MAT * ORTHO = ORTHO * MAT.
( (x2-x1)/2| 0 | 0 |(x1 + x2)/2 )
( 0 |(y2-y1)/2| 0 |(y1 + y2)/2 )
MAT = ( 0 | 0 |(z2-z1)/2|(z1 + z2)/2 )
( 0 | 0 | 0 | 1 )
Es ist det(MAT) = (x2-x1)*(y2-y1)*(z2-z1)/8,
( 2/(x2-x1)| 0 | 0 |(x1 + x2)/(x2-x1) )
( 0 |2/(y2-y1)| 0 |(y1 + y2)/(y2-y1 )
ORTHO = ( 0 | 0 |2/(z2-z1)|(z1 + z2)/(z2-z1) )
( 0 | 0 | 0 | 1 )
Es ist det(ORTHO) = 8 /((x2-x1)*(y2-y1)*(z2-z1)).
Ist t die Transposition undMAT * E1 = P1, ORTO * P1 = E1, MAT * E2 = P2, ORTO * P2 = E2.
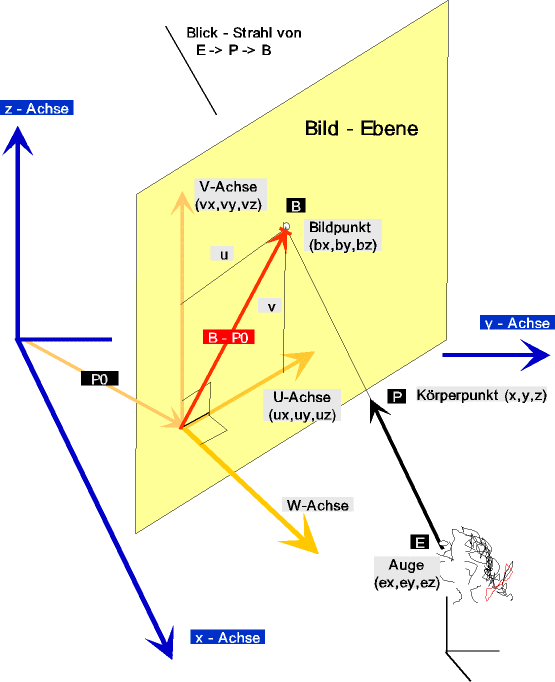
In dem folgenden Bild sind die Bezeichnungen enthalten. Große Buchstaben sind 3D - Vektoren. Kleine Buchstaben skalare Werte ( Koordinaten ). Alle 3D - Raumpunkte werden in einem kartesischen x,y,z - Koordinatensystem angegeben. Die Körperpunkt werden mit P(x,y,z) bezeichnet. Der Körper besteht aus vielen 3D - Punkten. Diese Punkte werden auf die Bild - Ebene projiziert. Dann entsteht in dieser Eben das Bild des Körpers. Die Bild - Ebene ist durch die orthogonalen Einheitsvektoren U, V, W und den Bild - Bezugspunkt P0(x0,y0,z0) festgelegt. Wenn U, V, W, P0, E, P gegeben sind, so sollen nun
Das Auge ( Eye ) entspricht dem Projektionszentrum ( Zentalprojektion ). Vom Auge E(ex,ey,ez) geht der Blickstrahl zu einem Körper - Punkt P(x,y,z).
Der Blickstrah durchstößt im Punkt B die Bild - Ebene. In der Geraden - Gleichung
B = E + t . ( P - E ) oder
( B - P0 ) = ( E - P0 ) + t . ( P - E )
ist B und t unbekannt. Weil ( B - P0 ) in der Zeichenebene liegt und damit senkrecht zu W ist, wird das
Skalarprodukt "o" dieser Gleichung mit W gebildet.
( B - P0 ) o W ist 0.
0 = ( E - P0 )o W + t . ( P - E ) o WDarau ergibt sich der gesuchte Geraden - Parameter t des Bild - Punktes B zu
( P0 - E ) o W
t = ----------------
( P - E ) o W
Mit t kann ( B - P0 ) berechnet werden. Die u,v - Koordinaten in der Zeichenebene
ergeben sich als Skalarprodukt von ( B - P0 ) mit dem Einheisvektoren U, V gemäß
( P0 - E ) o W
t = ---------------- ,
( P - E ) o W
u = U o ( B - P0 ) = U o { ( E - P0 ) + t . ( P - E ) },
v = V o ( B - P0 ) = V o { ( E - P0 ) + t . ( P - E ) }
Zu einem gegebenen Körperpunkt P(x,y,z) kann zunächst t und dann u,v berechnet werden. Die Abbildung versagt, wenn das Auge in der Bildebene liegt oder ein Körperpunkt P im Auge E ist.
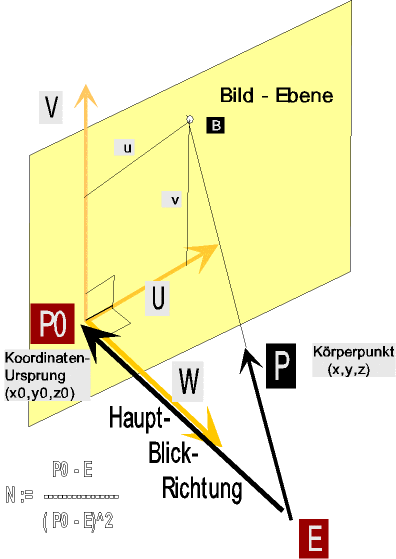
Die obigen Formeln sind vielseitig und flexibel. Nun sollen die ( mühsamen ) Vorüberlegungen zu den U, V, W - Vorgaben vereinfacht werden. Die Netzhaut des Auges ist "senkrecht" zur Haupt - Blickrichtung. Die Haupt - Blickrichtung ist die Richtung vom Auge zur Bildmitte P0.
( P0 - E ) o W ( P0 - E ) o N
t = ---------------- = ----------------
( P - E ) o W ( P - E ) o N
Vd ist ein ( willkürlicher ) Vektor für die "(V)ertikale (d)irection". Z.B. kann Vd = ( 0.0, 1.0, 0.0 ) gewählt werden. Ist E, P0, Vd gegeben, so können die Einheitsvektoren U, V, W berechnet werden gemäß
( P0 - E )
N := -------------
( P0 - E )2
U := N x Vd, U := U / | U | ,
V := U x N , V := V / | V | ,
W := U x V
Diese Berechnung der Einheitsvektoren U, V, W ist nur einmal erforderlich. Danach sind viele Körperpunkte P(x,y,z) in die Koordinaten u,v der Zeichen - Ebene umzurechnen.
nn := N o ( P - E ), Fehler, falls nn == 0 ist uu := U o ( P - E ), u = uu / nn vv := V o ( P - E ), v = vv / nn
Durch "o" wird das Skalarprodukt gekennzeichnt. Je Körperpunkt P sind 9 Multiplikationen und 2 Divisionen erforderlich.
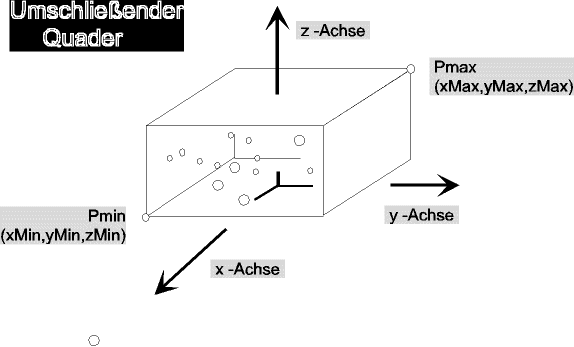
Zur Beschreibung eines 3D - Körpers werden Punkte P(x,y,z) verwendet. Mit Hilfe dieser Punkte werden die Körper beschrieben. Alle gegebene Punkte liegen in einem umschließenden Quader. Die Bildebene soll so angeordnet werden, daß der Mittelpunkt P0(x0,y0,z0) der Bildebene gleich dem Mittelpunkt des umschließenden Quaders ist.
Zum besseren Vorstellen seien lediglich 4 Punkte Pk(xk,yk,zk) mit k = 0, 1, 2, 3 in einer Punkte - Tabelle gegeben.
| k | x[k] | y[k] | z[k] | Bemerkungen |
| 0 | 17.3 | 5.1 | 6.2 |
Indem alle xk durchgegangen werden ergeben sich xMin, xMax. Indem alle yk durchgegangen werden ergeben sich yMin, yMax. Indem alle zk durchgegangen werden ergeben sich zMin, zMax. |
| 1 | -1.3 | -6.1 | 13.3 | |
| 2 | 51.5 | -55.5 | -0.5 | |
| 3 | 31.1 | -33.3 | -0.3 | |
| xMin | yMin | zMin | ||
| xMax | yMax | zMax |
Alle Körper - Punkte Pk liegen in dem umschließenden Pmin, Pmax - Quader. Der Quader - Mittelpunkt P0 und die halbe Quader - Dagonale R ist dann
P0 = ( Pmax + Pmin ) / 2 , R = ( Pmax - Pmin ) / 2
Der Rand - Blickstrahl berührt die umschließende Kugel tangential. Deshalb ist R etwas zu vergrößern, damit alle Punkte Pk in der
erscheinen. Aus dem umschließenden Pmin, Pmax - Quader kann die ( kleinste ) Größe der Bild - Ebene berechnet werden:
P0 = ( Pmax + Pmin ) / 2 ,
R = ( Pmax - Pmin ) / 2 ,
r = | R | , e = | P0 - E | , e > r ,
r . e
rr = -------------------------------
sqrt( ( e - r ) . ( e + r ) )
uMin = -rr , uMax = +rr ,
vMin = -rr , vMax = +rr
Sind alle Körper - Punkte Pk und die Position E des Auges bekannt, so kann der Reihe nach Pmin, Pmax, P0, R, r, e, rr, uMin, vMin, uMax, vMax berechnet werden. Dann liegt auch die Haupt - Blick - Richtung N fest und mit Vd auch U, V, W fest. Die Zentalprojektion ( 4x4 Matrix ) kann durchgeführt werden. Alle 3D - Punkte Pk erscheinen in der ( u, v ) Bilde - Ebene.
GL nutzt im Projektionsraum nach glMatrixMode(GL_PROJECTION); glLoadIdentity(); die Funktionen:gluPerspective( GLdouble fovy, // y-Oeffnungswinkel in Grad GLdouble aspect, // = (GLfloat)w/(GLfloat)h; GLdouble zNear, // pos. vordere Clip-Entfernung GLdouble zFar // pos. hintere Clip-Entfernung ); // und gluLookAt( Ex,Ey,Ez, P0x,P0y,P0z, Vdx,Vdy,Vdz );
Beim ändern der Viewport-Grösse ( h,w ) wird die CALLBACK-Funktion ChangeSize() aufgerufen. Ist der begrenzender Quader global durch (xMin,yMin,zMin),(xMax,yMax,zMax) und der sollvBlickwinkel ( z.B. = 65.0 Grad ) gegeben, so kann bei GL die geeignete Projektion errechnet werden: GL_PROJECTION: glLoadIdentity(), gluPerspective() mit nachfolgendem GL_MODELVIEW: glLoadIdentity(), glTranslated(0,0,-viewDist).
static void CALLBACK ChangeSize(GLsizei w, GLsizei h)
{ if(h == 0)h = 1;
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
glViewport(0, 0, w, h);
if(PARALLELPROJEKTION) {
if (w <= h) {
glOrtho(xMin,xMax, yMin*h/w,yMax*h/w, zMin,zMax);
} else {
glOrtho(xMin*w/h,xMax*w/h, yMin,yMax, zMin,zMax);
}
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
} else
if(ZENTRALPROJEKTION) {
double dx = (xMax-xMin)/2;
double dy = (yMax-yMin)/2;
double dz = (zMax-zMin)/2;
double r = sqrt(dx*dx+dy*dy+dz*dz);
double t = fabs(tan(sollvWinkel*PI/360));
double e = r/t; if( e < r ) e = r;
e *= 1.05;
double rr = r*e/sqrt((e-r)*(e+r));
double ee = rr/t;
double zNear = 0.9*ee;
double zFar = (ee + rr + rr)/0.9;
double viewAspect = (double)w/(double)h;
gluPerspective(sollvWinkel,viewAspect,zNear,zFar);
glMatrixMode(GL_MODELVIEW); glLoadIdentity();
glTranslated(0.0,0.0,-(zNear+zFar)/2);
}
}
Die obigen Formel können in eine 4x4 - Matrix übertragen werden. Die Skalar - Produkte NoE, UoE, VoE werden einmal berechnent.
( uu ) ( ux uy uz | - U o E) ( x ) ( vv ) ( vx vy vz | - V o E) ( y ) ( 0 ) = ( 0 0 0 | 0 ) . ( z ) ------ (-----------------|---------) ----- ( nn ) ( nx ny nz | - N o E ) ( 1 ) u := uu / nn v := vv / nn
P0 = ( 0, 0, 0 ), E = ( 0, 0, e ) aus. Der Reihe nach ergibt sich:
P0 := ( 0,0,0 ), E := ( 0,0,e ), U := ( 1,0,0 ), V := ( 0,1,0 ), W := ( 0,0,1 ), N = (P0-E)/(P0-E)2 = ( 0,0,-1/e ), N o E = -1, U o E = 0, V o E = 0, u = x / ( 1 - z/e ), v = y / ( 1 - z/e )
Wenn der zentrale Punkt E ins Unendliche wandert, so geht die Zentralprojektion in die Parallelprojektion über. Die Projektions - Formeln hängen dann nicht mehr von E ab.
( P0 - E ) o W
t = ---------------- ---> 1 ,
( P - E ) o W
u = U o ( P - P0 ) ,
v = V o ( P - P0 )
Es werden folgende Berechnungen durchgefuehrt:
Vd Vd = Vertikale Richtung
Wd = Eye - Org Wd = -Hauptblickrichtung
U = Vd x Wd U = U / |U|
V = Wd x U V = V / |V|
W = Wd /|Wd|/|Wd|, W hat gleiche Richtung wie Wd !
if ( Eye == NULL ) Eye = MAT_set_vec( & Eye, 0.0, 0.0, -1.0/EPSILON ) ;
if ( Org == NULL ) Org = MAT_set_vec( & OO, 0.0, 0.0, 0.0 ) ;
if ( Vd == NULL ) Vd = MAT_set_vec( & VV, 0.0, 1.0, 0.0 ) ;
Wd.x = Eye.x - Org.x ;
Wd.y = Eye.y - Org.y ;
Wd.z = Eye.z - Org.z ;
h2 = fabs( Wd.x * Wd.x + Wd.y * Wd.y + Wd.z * Wd.z ) ;
if ( h2 < EPSILON ) { //Setze irgendwas, trotz Fehler!
Eye.x = -1.0/EPSILON ; Eye.y = -2.0/EPSILON ; Eye.z = -10.0/EPSILON ;
Wd.x = Eye.x - Org.x ;
Wd.y = Eye.y - Org.y ;
Wd.z = Eye.z - Org.z ;
h2 = fabs( Wd.x * Wd.x + Wd.y * Wd.y + Wd.z * Wd.z ) ;
}
if ( h2 < EPSILON ) goto MAT_set_projErr ;
MAT_vec_cross_prod( U, Vd, Wd ) ; isOk = MAT_vec_norm( U );
if ( ! isOk ) {//Setze irgendwas, trotz Fehler!
Vd.x = fabs( Wd.z ) + fabs( Wd.y ) ; Vd.y = fabs( Wd.x ) + fabs( Wd.z ) ; Vd.z = fabs( Wd.y ) + fabs( Wd.x ) ;
MAT_vec_cross_prod( U, Vd, Wd ) ; isOk = MAT_vec_norm( U );
}
MAT_vec_cross_prod( V, Wd, U ) ; isOk &= MAT_vec_norm( & V );
W.x = Wd.x / h2 ;
W.y = Wd.y / h2 ;
W.z = Wd.z / h2 ;
if ( ! isOk ) goto MAT_set_projErr ;
//memset( & Mat, 0, sizeof( RMAT4X4 ) ) ;
MAT_vec_scalar_prod ( h2, W, Eye ) ; Mat[0][0] = +h2 ;
MAT_vec_scalar_prod ( h2, U, Eye ) ; Mat[1][0] = -h2 ;
MAT_vec_scalar_prod ( h2, V, Eye ) ; Mat[2][0] = -h2 ;
Mat[0][1] = -W.x ; Mat[0][2] = -W.y ; Mat[0][3] = -W.z ;
Mat[1][1] = +U.x ; Mat[1][2] = +U.y ; Mat[1][3] = +U.z ;
Mat[2][1] = +V.x ; Mat[2][2] = +V.y ; Mat[2][3] = +V.z ;
//Alternative 1
Mat[3][0] = Mat[3][1] = Mat[3][2] = Mat[3][3] = 0.0 ;
//?Alternative 2, W sollte Einheitsvektor, h2 ?
//Mat[3][0] = -h2 ; Mat[0][1] = W.x ; Mat[3][2] = W.y ; Mat[3][3] = W.z ;
pRMAT4X4_EXT = MAT_set_4x4( idx, & Mat ) ;
In OpenGL können auch eigene Transformationen eingebaut werden. Soll z.B. anstelle einer Zentralprojektion auf eine Ebene auf eine Kugeloberfläche projiziert werden, so sind folgende Überlegungen hilfreich:
Blickstrah B = A + t.( K-A) wird in Kugel ( B-w)2 = R2 ergibt eingesetzt: t2 + t.2( A-W)o( K-A) + ((A-W)2 - R2)/(K-A)2 = 0 und liefert mit Wa := W - A, Ka := K - A h1 := Wa . Ka / Ka2 h2 := (R2-Wa2) . Ka2 / ( Wa . Ka )2 und damit den 3D-Bildpunkt B: t := h1 + ( 1+- sqrt(1+h2) ), B = A + t . Ka